Обзор: Американский математик построил граф (на илл.),
Американский математик построил граф (на илл.), радиус которого меньше, чем у коспектрального с ним графа четырёхмерного гиперкуба.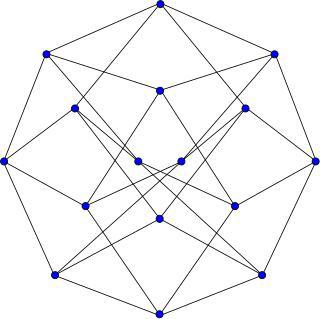
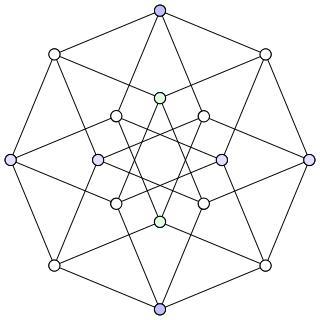
Граф Хоффмана является 4-регулярным графом с 16 вершинами и 32 рёбрами, который открыл Алан Хоффман и опубликовал в 1963. Граф коспектрален графу гиперкуба Q4.
Спектральная теория графов — направление в теории графов, изучающее свойства графов, характеристических многочленов, собственных векторов и собственных значений матриц, связанных с графом, таких, как его матрица смежности или матрица Кирхгофа.
В теории графов графом гиперкуба Qn называется регулярный граф с 2n вершинами, 2n−1n рёбрами и n рёбрами, сходящимися в одной вершине. Его можно получить как одномерный скелет геометрического гиперкуба. Например, Q3 — это граф, образованный 8 вершинами и 12 рёбрами трёхмерного куба. Граф можно получить другим образом, отталкиваясь от семейства подмножеств множества с n элементами путём использования в качестве вершин все подмножества и соединением двух вершин ребром, если соответствующие множества отличаются только одним элементом.
Алан Джером Хоффман — американский математик, сотрудник Исследовательского центра Т. Дж. Уотсона компании IBM. Редактор и основатель журнала англ. Linear Algebra and its Applications. Он внес вклад в комбинаторную оптимизацию и теорию собственных значений графов. Хоффман совместно с Робертом Синглтоном построил граф Хоффмана — Синглтона, который является уникальным графом Мура степени 7 и диаметра 2.
Метрика кратчайшего пути — метрика на вершинах графа равная числу рёбер в кратчайшем пути между даннымми вершинами. Если нет пути между двумя вершинами, то есть если они принадлежат различным компонентам связности, то принято считать расстояние бесконечным.
Теги: Хоффман, Алан Граф Хоффмана Расстояние (теория графов) Спектральная теория графов Граф гиперкуба Американский математик построил граф радиус которого меньше графа